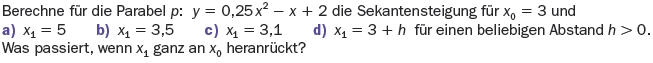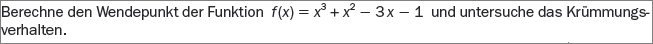Workshop GeogebraCAS - Differentialrechnung Grundlagen
Vorübungen
Ex1: Graphisches Differenzieren
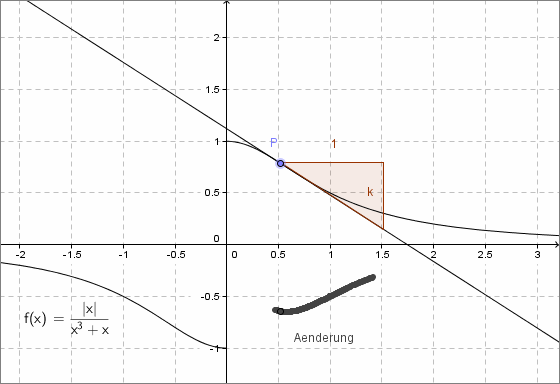
Erstellen Sie ein Geogebra-Arbeitsblatt, dass es den Schülerinnen und Schülern ermöglicht, graphisch Funktionen abzuleiten.
Entwickeln Sie Ihr Arbeitsblatt mit der Funktion <tex>f(x)=x^2</tex>
und testen Sie es mit den Funktionen <tex>f(x)= \root 3 \of {x^2}</tex>, <tex>f(x)= \frac{|x|}{x\cdot (x^2+1)}</tex>
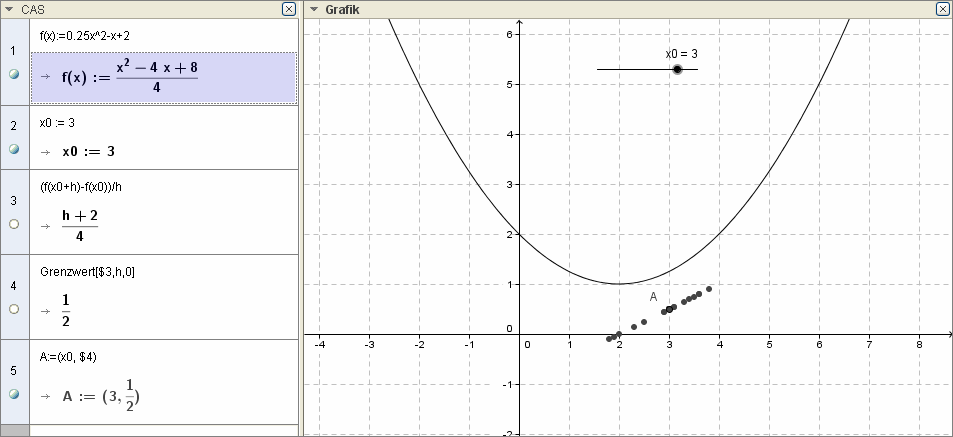
Ex2: Von der Sekantensteigung zur Tangentensteigung
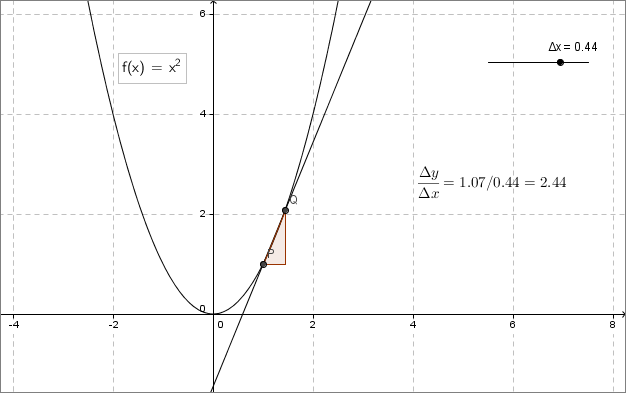
Erstellen Sie ein Geogebra-Arbeitsblatt, dass es den Schülerinnen und Schülern ermöglicht, über einen Schieberegler die Größe eines Steigungsdreiecks zu verändern. Die Steigung des Dreiecks bzw. der Sekante soll dabei über einen Schieberegler gesteuert werden können und auch angezeigt werden.
Vom Differenzen- zum Differentialquotienten
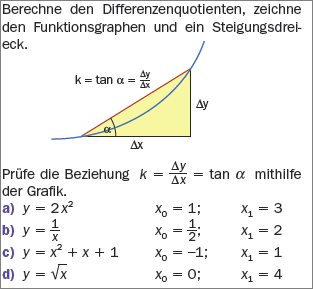
Ex3: Differenzenquotient 1
Ex4a: Differenzenquotient 2
Ex5: Differenzenquotient 3
Ex6: Differentialquotient 1
Ermittle für <tex>f(x)=0,25 x^2 - x +2</tex> den Differentialquotienten an der Stelle 3.
Ex7: Differentialquotient 2
Geben Sie eine beliebige Funktion <tex>f(x)</tex> vor und zeichnen Sie mit dem Stift-Werkzeug den Graphen der Ableitungsfunktion ein.
Vergleichen Sie die eingezeichnete Ableitung mit der tatsächlichen Ableitungsfunktion, die sie mittels <tex>f'(x)</tex> oder Ableitung(f) erhalten.
Siehe auch folgende BIFIE-Übungsaufgabe
Untersuchen und Ermitteln von Funktionen
Ex8: Untersuchen von Funktionen 1
Hinweis: Verwenden Sie dazu den Befehl Lösungen[].
Ex9: Untersuchen von Funktionen 2
Hinweis: Zum Untersuchen von Funktionen eignet sich auch das Werkzeug Funktionsinspektor.
Ex10: Untersuchen von Funktionen 3
Gib die größtmögliche Definitionsmenge der Funktion <tex>f(x) = \frac{2x^2 − 3x − 1}{2 \cdot (x − 1)}</tex> an.
a) Ermittle ihre Nullstellen und zeichne ihren Graphen.
b) Gib die Gleichungen der Asymptoten an.
Ex11: Auffinden von Polynomfunktionen
Stellen Sie die entsprechenden Gleichungen auf und lösen Sie mit dem Befehl Löse[{Liste der Gleichungen},{Liste der Variablen}]
Ex12: Lösen einer Differentialgleichung
Exakte Lösung: Verwenden Sie dazu in der CAS-Ansicht den Befehl LöseDGL(Gleichung,abhängige Variable, unabhängige Variable)
Numerische Lösung:
- Erzeugen Sie einen Startpunkt
- Verwenden Sie dazu in der Algebra-Ansicht den Befehl
LöseDGL(Rechte Seite der Differentialgleichung,x-Koordinate des Startpunkts, y-Koordinate des Startpunkts, Endwert für x, Schrittweite) - Um ein Richtungsfeld zu erzeugen verwenden Sie den Befehl
Richtungsfeld(Rechte Seite der Differentialgleichung)
Editierhilfe
