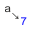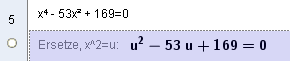Dies ist eine alte Version des Dokuments!
Variablen und Terme
<box> Mithilfe des Computeralgebrasystems (CAS) von GeoGebra lassen sich Terme umformen. Einerseits kannst du dabei Schritt für Schritt vorgehen (wie du am Papier arbeiten würdest), andererseits steht dir eine Reihe von geeigneten Befehlen zur Verfügung. </box>
Term expandieren
Werkzeug  | Werkzeug  | Befehl Multipliziere[] |
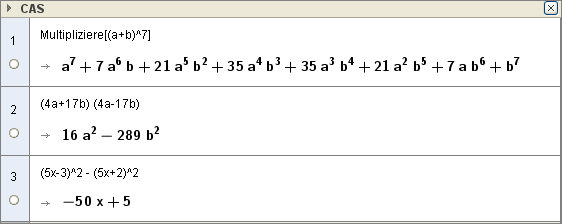
Ex1: Rechne die folgenden Terme aus und kontrolliere dein Ergebnis mittels CAS:
a) $(a+b)^7 =$
b) $(4a+17b)\cdot(4a-17b) = $
c) $(5x-3)^2 - (5x+2)^2 =$
Term faktorsieren
Werkzeug  | Befehl Faktorisiere[] |
Ex2: Verwandle mittels CAS in die Produktdarstellung und kontrolliere durch Ausrechnen:
a) $x^4-1 =$
b) $x^5+1=$
c) $x^4+2x^3-3x^2-8x-4 =$
Vollständiges Quadrat
- VollständigesQuadrat(<quadratische Funktion>) … Gibt eine quadratische Funktion in Form eines vollständigen Quadrates `a(x−m)^2+n` an.
Ex3: Ermittele die Koordinaten der Scheitelpunkte der folgenden Parabeln
a) `p_1(x)= x^2-15x+56`
b) `p_2(x)= 3x^2-15x+56`
Bruchterme
Ex4 a) Vereinfache den Bruchterm indem du die Division ausführst: `(6x^3-5x^2+9x+10):(3x+2)`
<tab>b) Dividiere und überprüfe das Ergebnis der Division: `(10x^2-29x+10):(2x-3)`
Partialbruchzerlegung
- Partialbruch(<Bruchterm>) … Gibt die Partialbruchzerlegung des angegebenen Bruchterms an, wenn möglich.
Substituieren in Termen
Werkzeug  | Befehl Ersetze[] |
Ex5 Die Schwingungsdauer `T` eines Pendels der Länge `l` beträgt `T=2\pi \sqrt(l/g)`.
Ersetze in der Formel die Pendellänge durch `l` durch 15m und die Schwerebeschleunigung `g` durch `9,81 m/s`.
Ex6 Führe die Gleichung `x^4-53 x^2 +196=0` durch Substitution auf eine quadratische Gleichung zurück!
`x^4-53 x^2 +196=0`
Variable
Variable, Wert und Schieberegler
Variable können in Geogebra ohne Werte sein oder mit einem Wert belegt werden. Mit einem defnierenden Doppelpunkt und einem Gleichheitszeichen wird einer Variable ein Wert zugewiesen. Wird auf den Sichtbarkeitspunkt geklickt, so erscheint im Graphikfenster ein Schieberegler mit dem der Wert der Variablen verändert werden kann.
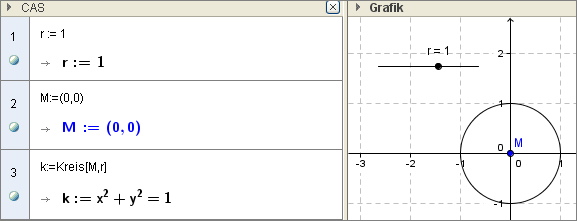
Ex7: Weise der Variablen $r$ den Wert 1 zu, definiere einen den Punkt $M$ mit den Koordinaten (0,0) und erstelle einen Kreis mit Radius $r$ und Mittelpunkt $M$.
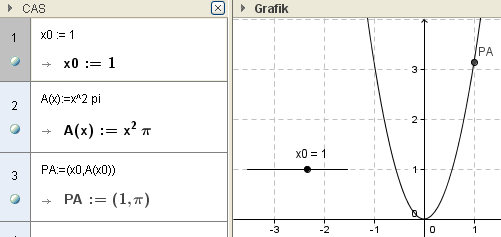
Ex8: Weise der Variablen $x_0$ den Wert 1 zu, definiere die Flächeninhaltsfunktion $A(x):=x^2 \pi$ und lassen einen Punkt auf der Funktion in Abhängigkeit von der unabhängigen Variablen $x_0$ wandern.
Variable löschen
Mittels Leerdefinition (zB. 'a:=') oder mit Befehl Lösche(var),
Editierhilfe
