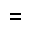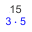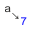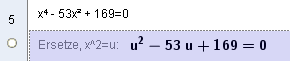Variablen und Terme
<box> Mithilfe des Computeralgebrasystems (CAS) von GeoGebra lassen sich Terme umformen. Einerseits kannst du dabei Schritt für Schritt vorgehen (wie du am Papier arbeiten würdest), andererseits steht dir eine Reihe von geeigneten Befehlen zur Verfügung. </box>
Term expandieren
Werkzeug  | Werkzeug  | Befehl Multipliziere[] |
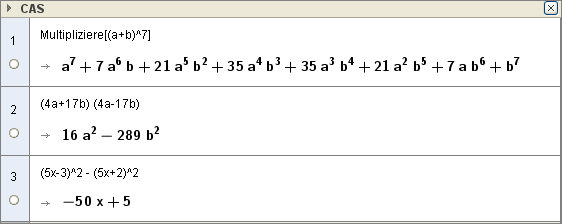
Ex1: Rechne die folgenden Terme aus und kontrolliere dein Ergebnis mittels CAS:
a) $(a+b)^7 =$
b) $(4a+17b)\cdot(4a-17b) = $
c) $(5x-3)^2 - (5x+2)^2 =$
Term faktorsieren
Werkzeug  | Befehl Faktorisiere[] |
Ex2: Verwandle mittels CAS in die Produktdarstellung und kontrolliere durch Ausrechnen:
a) $x^4-1 =$
b) $x^5+1=$
c) $x^4+2x^3-3x^2-8x-4 =$
Vollständiges Quadrat
- VollständigesQuadrat(<quadratische Funktion>) … Gibt eine quadratische Funktion in Form eines vollständigen Quadrates `a(x−m)^2+n` an.
Ex3: Ermittele die Koordinaten der Scheitelpunkte der folgenden Parabeln
a) `p_1(x)= x^2-15x+56`
b) `p_2(x)= 3x^2-15x+56`
Bruchterme
Ex4 a) Vereinfache den Bruchterm indem du die Division ausführst: `(6x^3-5x^2+9x+10):(3x+2)`
<tab>b) Dividiere und überprüfe das Ergebnis der Division: `(10x^2-29x+10):(2x-3)`
Partialbruchzerlegung
- Partialbruch(<Bruchterm>) … Gibt die Partialbruchzerlegung des angegebenen Bruchterms an, wenn möglich.
Substituieren in Termen
Werkzeug  | Befehl Ersetze[] |
Ex5 Die Schwingungsdauer `T` eines Pendels der Länge `l` beträgt `T=2\pi \sqrt(l/g)`.
Ersetze in der Formel die Pendellänge durch `l` durch 15m und die Schwerebeschleunigung `g` durch `9,81 m/s`.
Ex6 Führe die Gleichung `x^4-53 x^2 +196=0` durch Substitution auf eine quadratische Gleichung zurück!
`x^4-53 x^2 +196=0`
Variable
Variable, Wert und Schieberegler
Variable können in Geogebra ohne Werte sein oder mit einem Wert belegt werden. Mit einem defnierenden Doppelpunkt und einem Gleichheitszeichen wird einer Variable ein Wert zugewiesen. Wird auf den Sichtbarkeitspunkt geklickt, so erscheint im Graphikfenster ein Schieberegler mit dem der Wert der Variablen verändert werden kann.
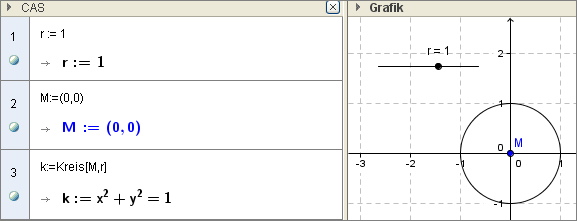
Ex7: Weise der Variablen $r$ den Wert 1 zu, definiere einen den Punkt $M$ mit den Koordinaten (0,0) und erstelle einen Kreis mit Radius $r$ und Mittelpunkt $M$.
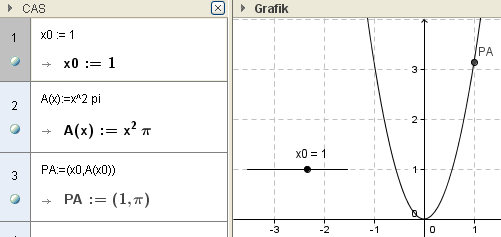
Ex8: Weise der Variablen $x_0$ den Wert 1 zu, definiere die Flächeninhaltsfunktion $A(x):=x^2 \pi$ und lassen einen Punkt auf der Funktion in Abhängigkeit von der unabhängigen Variablen $x_0$ wandern.
Variable löschen
Mittels Leerdefinition (zB. 'a:=') oder mit Befehl Lösche(var),
Variablenkonzept
Das Variablenkonzept unter Geogebra ist grundsätzlich anders als unter Derive (was insbesondere bisherigen Derive-NutzerInnen Probleme bereitet).
- Variablen sind geschützt
- Jede Variable wird in Geogebra genau einmal definiert und kann später nur am Ort ihrer Definition geändert werden (was dann zu einer Änderung aller davon abhängigen Berechnungen führt).
- Ist eine Variable bereits definiert und wird versucht sie an anderer Stelle nochmals zu definieren, wird dies vom System verweigert (und der nächste freie Variablenname statt dessen genommen).
- wird ein Ausdruck im CAS eingegeben aber keinem Namen zugewiesen, so erfolgt auf jeden Fall beim Zeichnen dieses Ausdrucks (über den links befindlichen Kreis „Marbel“, sofern überhaupt ein plotbarer Ausdruck vorliegt) eine Zuweisung an einen (freien) Variablenbuchstaben.
- Variablendefinition im Algebra-Fenster
Variablen, die im Algebra-Fenster definiert werden, erscheinen im CAS-Fenster nicht. Sie sind dort aber bekannt und können daher verwendet werden.
- Variablendefinition im CAS-Fenster
Ausdrücke, die im CAS-Fenster verwendet werden, erscheinen im Algebra-Fenster dann, wenn sie
a) als Variablendefinition in der Form „Variablenname:= Wert“ (z.B. A:= 2 pi) eingegeben werden oder
b) wenn sie plotbar sind. Dann wird ihnen beim Plotten (über den Sichtbarkeitsschalter „Marbel“) ein (freier) Variablenname zugewiesen (zb: c:=x^2+y^2=1)
Die Eingabe m:=u erscheint nur dann im Algebrafenster, wenn u einen Wert besitzt (und damit plottbar ist).
- Dynamischer und statischer Bezug auf bereits definierte Variable
a) Bei der Verwendung von Variablennamen oder $Zeilennummer erfolgt ein dynamischer Bezug.
b) Bei der Verwendung von #Zeilennummer erfolgt ein statischer Bezug.
Ex9: Definiere die Kreisumfangsformel mittels dynamischen und statischen Bezug auf den Radius
Eingabe:
Nun wird in der 1. Zeile der Wert von r auf 3 geändert:
Wie man sieht, wurden die dynamisch definierten Zeilen #3 bzw. #5 geändert, während Ausdruck #7 (der über statische Bezug zustande gekommen ist) unverändert blieb.
Eine Möglichkeit, den dynamischen Bezug auf Variablen grundsätzlich auszuschalten gibt es nicht. Dies wäre auch gar nicht sinnvoll, da ja ohnehin ein statischer Bezug auch möglich ist.